Skip to content

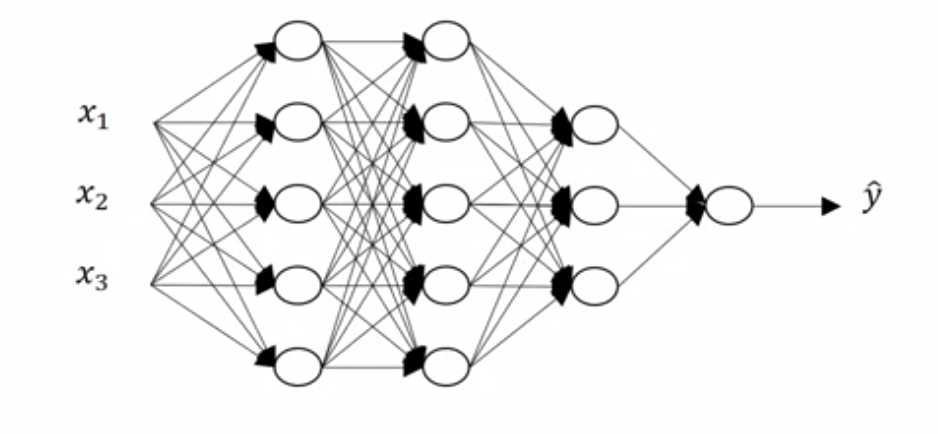
Week 4 — L Layers Deep Neural Networks

Computation of L layered neural network

May 6, 2021

New notations introduces

  • $L$ to denote the number of layers in the network

In previous week example $L = 2$ - $n^{[l]}$ to denote the number of units/neurons in the layer $l$

In previous week example $n^{[1]} = 4, \, n^{[0]} = n_x = 3$

Forward Propagation in a Deep Network

Let's go over what forward propagation will look like for a single training example $x$ (which is also $a^{[0]}$).

$z^{[1]} = W^{[1]}a^{[0]}+b^{[1]}$

$a^{[1]} = g^{[1]}(z^{[1]})$

$z^{[2]} = W^{[2]}a^{[1]}+b^{[2]}$

$a^{[2]} = g^{[2]}(z^{[2]})$

$\qquad....$

$z^{[4]} = W^{[4]}a^{[3]} + b^{[4]}$

$a^{[4]} = \hat{y} = g^{[4]}(z^{[4]})$

Generally equation for the forward propagation of any layer l

$z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}$

$ a^{[l]} = g^{[l]}(z^{[l]})$

Vectorizing over whole training set or m training example

$Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}$

$A^{[l]} = g^{[l]}(Z^{[l]})$

Here $A^{[0]}$ is going to be $X$.

Getting your matrix dimensions right

Warning

In the this video, at time 6:35, the correct formula should be:

$a^{[l]} = g^{[l]}(z^{[l]})$

Note that "a" and "z have dimensions $(n^{[l]},1)$.

  • Check the dimension of the matrix $W^{[l]}$ as to be $(n^{[l]}, n^{[l-1]})$
  • and dimension of $X$ or $A^{[0]}$ to be $(n^{[0]}, m)$.
  • The dimension of the matrix $b^{[l]}$ to be $(n^{[l]},1)$
  • The dimension of $Z^{[l]}$ and $A^{[l]}$ to be $(n^{[l]}, m)$
  • The dimension of $dW^{[l]}$ be $(n^{[l]}, n^{[l-1]})$.
  • The dimension of $db^{[l]}$ be $(n^{[l]}, 1)$
  • The dimension of $dZ^{[l]}$ and $dA^{[l]}$ be $(n^{[l]}, m )$.

Why deep representations?

Deep representations help in generating lower level features which can then be used to build and then composing these features in later layer of NN to create higher level features and understand complex functions.

Circuit theory and deep learning

Informally: There are functions you can compute with a "small" L-layer deep neural network that shallower networks require exponentially more hidden units to compute.

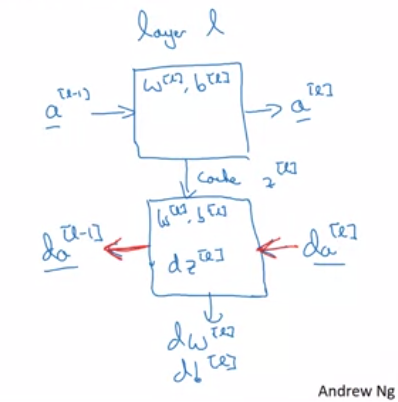
Building blocks of deep neural networks

We have already seen the forward propagation for the $L$ layers neural network in which we cached $Z^{[l]}$.

The the backward step would be like to calculate $dA^{[l-1]},\enspace dZ^{[l]},\enspace dW^{[l]}.\enspace db^{[l]}$ with input as cache and $dA^{[l]}$.

Forward and Backward Propagation

Warning

Note that in the next video at 2:30, the text that's written should be $dw^{[l]} = dz^{[l]} * a^{[l-1]\bold{\top}}$

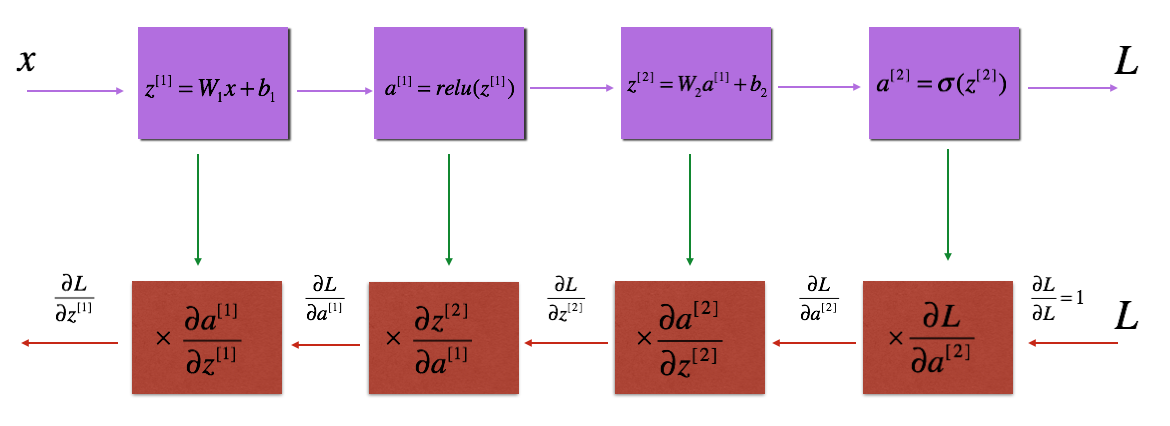
Forward and backward propagation. Source: Coursera Assignment

To output $dA^{[l-1]},\enspace dZ^{[l]},\enspace dW^{[l]}.\enspace db^{[l]}$; we do:

$dZ^{[l]} = dA^{[l]}* g'^{[l]}(Z^{[l]})$

$dW^{[l]}=\frac{1}{m}dZ^{[l]}.A^{[l-1]\bold{\top}}$

$db^{[l]}=\frac{1}{m}\text{np.sum($dZ^{[l]}$, axis=1, keepdims=True)}$

$dA^{[l-1]}=W^{[l]\bold{\top}}dZ^{[l]}$

$dAL = -(\text{np.divide($Y, AL$)} - \text{np.divide($1-Y$, $1-AL$)}$

Parameters VS Hyperparameters

Parameters are values that the neural net needs to learn by itself such as $W$ and $b$.

Hyperparameters are the extra values we decide and that we give it that it needs to run - the learning rate, the number of iterations of gradient descent, the number of hidden layers, the number of hidden units in each layer, and the choice of activation function.

We call these hyperparameters since these influence the actual parameters that the neural net is responsible for calculating.