Maths Formula Compendium

Trigonometry

Name	$0\degree$	$30\degree (\frac{\pi}{6})$	$45\degree (\frac{\pi}{4})$	$60\degree (\frac{\pi}{3})$	$90\degree (\frac{\pi}{2})$	$120\degree (\frac{2\pi}{3})$	$135\degree (\frac{3\pi}{4})$	$150\degree (\frac{5\pi}{6})$	$180\degree (\pi)$
$\sin$	$0$	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	$0$
$\cos$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	$0$	$-\frac{1}{2}$	$-\frac{1}{\sqrt{2}}$	$-\frac{\sqrt{3}}{2}$	$-1$
$\tan$	$0$	$\frac{1}{\sqrt{3}}$	$1$	$\sqrt{3}$	$\infin$	$-\sqrt{3}$	$-1$	$-\frac{1}{\sqrt{3}}$	$0$
$\cot$	$\infin$	$\sqrt{3}$	$1$	$\frac{1}{\sqrt{3}}$	$0$	$-\frac{1}{\sqrt{3}}$	$-1$	$\sqrt{3}$	$-\infin$
$\sec$	$1$	$\frac{2}{\sqrt{3}}$	$\sqrt{2}$	$ 2 $	$\infin$	$-2$	$-\sqrt{2}$	$-\frac{2}{\sqrt{3}}$	$-1$
$\cosec$	$\infin$	$2$	$\sqrt{2}$	$\frac{2}{\sqrt{3}}$	$1$	$\frac{2}{\sqrt{3}}$	$\sqrt{2}$	$2$	$\infin$

Trigonometric Identities

$\sin(A + B) = \sin A \cos B + \cos A \sin B$

$\sin(A - B) = \sin A \cos B - \cos A \sin B$

$\cos(A + B) = \cos A \cos B - \sin A \sin B$

$\cos(A - B) = \cos A \cos B + \sin A \sin B$

$\sin C + \sin D = 2 \sin \frac{C + D}{2} \cos \frac{C - D}{2}$

$\sin C - \sin D = 2 \cos \frac{C + D}{2} \sin \frac{C - D}{2}$

$\cos C + \cos D = 2 \cos \frac{C + D}{2} \cos \frac{C - D}{2}$

$\cos C - \cos D = -2 \sin \frac{C + D}{2} \sin \frac{C - D}{2}$

$\sin(A + B) \sin(A - B) = \sin^2 A - \sin^2 B$

$\cos(A + B) \cos(A - B) = \cos^2 A - \sin^2 B$

$\tan A - \tan B = \frac{\sin(A - B)}{\cos A \cos B}$

$\cot A - \cot B = \frac{-\sin(A - B)}{\sin A \sin B}$

$$ \sin(A + B + C) = \sin A \cos B \cos C + \cos A \sin B \cos C + \cos A \cos B \sin C - \sin A \sin B \sin C $$

$$ \cos(A + B + C) = \cos A \cos B \cos C - \cos A \sin B \sin C - \sin A \cos B \sin C - \sin A \sin B \cos C $$

$$ \tan(A + B + C) = \frac{\tan A + \tan B + \tan C - \tan A \tan B \tan C}{1 - \tan A \tan B - \tan B \tan C - \tan C \tan A} $$

Double Angle Formulas

$$ \begin{split} \sin 2A &= 2 \sin A \cos A \\ &= \frac{2 \tan x}{1 + \tan^2 x} \\ &= \frac{1 - \tan^2 A}{1 + \tan^2 A} \end{split} \newline\quad \begin{split}\cos 2A &= \cos^2 A - \sin^2 A \\& = 2\cos^2 A - 1 \\ &= 1 - 2\sin^2 \end{split} $$

$$ \sin 3A = 3 \sin A - 4 \sin^3 A \newline\quad \cos 3A = 4 \cos^3 A - 3 \cos A $$

$$ \tan 2A = \frac{2 \tan A}{1 - \tan^2 A} \newline\quad \tan 3A = \frac{3 \tan A - \tan^3 A}{1 - 3 \tan^2 A} $$

Product-to-Sum Formulas

• $2 \sin x \sin y = \cos(x - y) - \cos(x + y)$
• $2 \cos x \cos y = \cos(x + y) + \cos(x - y)$
• $2 \sin x \cos y = \sin(x + y) + \sin(x - y)$
• $2 \cos x \sin y = \sin(x + y) - \sin(x - y)$

Pythagorean Identities

• $\sin^2 \theta + \cos^2 \theta = 1$
• $1 + \tan^2 \theta = \sec^2 \theta$
• $1 + \cot^2 \theta = \csc^2 \theta$

$\tan(x + y) = \frac{\tan x + \tan y}{1 - \tan x \tan y}$

$\tan(x - y) = \frac{\tan x - \tan y}{1 + \tan x \tan y}$

$\cot(x + y) = \frac{\cot x \cot y - 1}{\cot x + \cot y}$

$\cot(x - y) = \frac{\cot x \cot y + 1}{\cot y - \cot x}$

• $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
• $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$

General Solutions

Basic Cases

• $\sin \theta = 0 \implies \theta = n\pi$
• $\cos \theta = 0 \implies \theta = (2n + 1)\frac{\pi}{2}$
• $\tan \theta = 0 \implies \theta = n\pi$

Equality Cases

• $\sin \theta = \sin \beta \implies \theta = n\pi + (-1)^n \beta$
• $\cos \theta = \cos \beta \implies \theta = 2n\pi \pm \beta$
• $\tan \theta = \tan \beta \implies \theta = n\pi + \beta$

Derived Cases

• $\sin^2 \theta = \sin^2 \beta \implies \theta = n\pi \pm \beta$
• $\cos^2 \theta = \cos^2 \beta \implies \theta = 2n\pi \pm \beta$
• $\tan^2 \theta = \tan^2 \beta \implies \theta = n\pi \pm \beta$

Secant and Cosine Properties

• $-\cos \theta = \cos(\pi - \theta)$
• $-\sec \theta = \sec(\pi - \theta)$
• $\cos(- \theta) = \cos\theta$
• $\sec(-\theta) = \sec\theta$

Transformation Rule (TR)

$(\frac{n\pi}{2} + \theta)$

• If $n$ is odd $\Rightarrow$ TR will change.

$(n\pi + \theta)$

• If $n$ is odd/even $\Rightarrow$ TR will not change.

Inverse Trigonometry

	Domain (value) ($x$)	Range (Angle) ($\theta$)
$sin^{-1}x$	$[-1,1]$	$[-\pi/2, \pi/2]$
$\cos^{-1}x$	$[-1. 1]$	$[0, \pi]$
$\tan^{-1}x$	$R$	$(-\pi/2, \pi/2)$
$\cot^{-1}x$	$R$	$(0, \pi)$
$\sec^{-1}x$	$R- (-1, 1)$	$[0, \pi-{\pi/2}$
$\cosec^{-1}x$	$R-(-1, 1)$	$[-\pi/2, \pi/2] - {0}$

Property 1	Property 2
$\sin^{-1}(\sin\theta) = \theta$	$\sin(\sin^{-1}x) = x$
$\cos^{-1}(\cos\theta) = \theta$	$\cos(\cos^{-1}x) = x$
$\tan^{-1}(\tan\theta) = \theta$	$\tan(\tan^{-1}x) = x$
$\cosec^{-1}(\cosec\theta) = \theta$	$\cosec(\cosec^{-1}x) = x$
$\sec^{-1}(\sec\theta) = \theta$	$\sec(\sec^{-1}x) = x$
$\cot^{-1}(\cot\theta) = \theta$	$\cot(\cot^{-1}x) = x$

Property 3
$sin^{-1}(-x) = -\sin^{-1}{x}$	$cos^{-1}(-x) = \pi -\cos^{-1}{x}$
$tan^{-1}(-x) = -\tan^{-1}{x}$	$cot^{-1}(-x) = \pi -\cot^{-1}{x}$
$cosec^{-1}(-x) = -\cosec^{-1}{x}$	$sec^{-1}(-x) = \pi -\sec^{-1}{x}$

Property 4
$sin^{-1}(\frac{1}{x}) = \cosec^{-1}x$
$cos^{-1}(\frac{1}{x}) = \sec^{-1}x$
$tan^{-1}(\frac{1}{x}) = \cot^{-1}x$

Property 5
$sin^{-1}x + \cos ^{-1}x = \frac{\pi}{2}$
$tan^{-1}x + \cot ^{-1}x = \frac{\pi}{2}$
$sec^{-1}x + \cosec ^{-1}x = \frac{\pi}{2}$

Property 6
$\sin^{-1}x + \sin^{-1}y = \sin^{-1} \big(x\sqrt{1-y^2} + y\sqrt{1-x^2}\big)$
$\sin^{-1}x - \sin^{-1}y = \sin^{-1} \big(x\sqrt{1-y^2} - y\sqrt{1-x^2}\big)$

Property 7
$\cos^{-1}x + \cos^{-1}y = \cos^{-1} \big(xy - \sqrt{1-x^2} \sqrt{1-y^2}\big)$
$\cos^{-1}x - \cos^{-1}y = \cos^{-1} \big(xy + \sqrt{1-x^2} \sqrt{1-y^2}\big)$

Property 8
$\tan^{-1}x - \tan^{-1}{y} = \tan^{-1}\Big(\frac{x+y}{1-xy}\Big)$
$\tan^{-1}x + \tan^{-1}{y} = \tan^{-1}\Big(\frac{x-y}{1+xy}\Big)$

Property 9

$2\sin^{-1}x = 2 \sin^{-1}(\theta/2)$

$3\sin^{-1}x = \sin^{-1}(3x-4x^2)$

$2\cos^{-1}x = \cos^{-1}(2x^2-1)$

$3\cos^{-1}x = \cos^{-1}(4x^3-3x)$

$$ 2 \tan^{-1}x = \tan^{-1}\Big(\frac{2x}{1-x^2}\Big) \\ 3\tan^{-1}x = \tan^{-1}\Big(\frac{3x-x^2}{1-3x^2}\Big) $$

Property 10

$$

2\tan^{-1}x = \begin{cases}\sin^{-1}\Big(\frac{2x}{1+x^2}\Big)\\cos^{-1}\Big(\frac{1-x^2}{1+x^2}\Big)\end{cases}

$$

---

$1-\cos\theta = 2 \sin^2(\theta/2)$

$1+ \cos\theta = 2\,\cos^2(\theta/2)$

$\sin\theta = 2\sin(\theta/2)\cos(\theta/2)$

$2\sin^{-1}x + \sin^{-1}(-x) = \cos^{-1}x$

$$ \begin{split}\cos2\theta &= \cos^2\theta - \sin^2\theta \\& = 2\cos^2\theta -1 \\ &= 1 - 2\sin^2\theta \end{split} $$

Expression and Substitution

Expression	Substitution	Substitution
$a^2 + x^2$	$x = a\tan\theta$	$x = a\cot\theta$
$a^2-x^2$	$x=a\sin\theta$	$x=a\cos\theta$
$x^2-a^2$	$x=a\sec\theta$	$x=a\cosec\theta$
$\sqrt{\frac{a-x}{a+x}}$	$x=a\cos2\theta$
$\sqrt{\frac{a^2+x^2}{a^2-x^2}}$	$x=a^2\cos2\theta$

Differentiation

$\frac{d}{dx} x^n = n x^{n-1}$

$\frac{d}{dx} a^x = a^x \ln a$

$\frac{d}{dx} \log_e x = \frac{1}{x}$

$\frac{d}{dx} \log_a x = \frac{1}{x \ln a}$

$\frac{d}{dx} e^x = e^x$

$\frac{d}{dx} \sin x = \cos x$

$\frac{d}{dx} \cos x = -\sin x$

$\frac{d}{dx} \tan x = \sec^2 x$

$\frac{d}{dx} \sec x = \sec x \tan x$

$\frac{d}{dx} \cot x = -\csc^2 x$

$\frac{d}{dx} \cosec x = -\cosec x \cot x$

$\log m^n = n \log m$

$\log m + \log n = \log (mn)$

$\log m - \log n = \log \left(\frac{m}{n}\right)$

$\log e = 1$, $\log_a a = 1$

$\log_a b = \frac{1}{\log_b a}$

$\frac{d}{dx} \sin^{-1} x = \frac{1}{\sqrt{1 - x^2}}$

$\frac{d}{dx} \cos^{-1} x = \frac{-1}{\sqrt{1 - x^2}}$

$\frac{d}{dx} \tan^{-1} x = \frac{1}{1 + x^2}$

$\frac{d}{dx} \cot^{-1} x = \frac{-1}{1 + x^2}$

$\frac{d}{dx} \sec^{-1} x = \frac{1}{x \sqrt{x^2 - 1}}$

$\frac{d}{dx} \cosec^{-1} x = \frac{-1}{x \sqrt{x^2 - 1}}$

• $a^{\log_a x} = x$
• $x^{\log_a y} = y^{\log_a x}$

Integration Formulas

Basic Integration Rules

1. $\int x^n \, dx = \frac{x^{n+1}}{n+1} + C$
2. $\int \frac{1}{x} \, dx = \ln x + C$
3. $\int e^x \, dx = e^x + C$
4. $\int a^x \, dx = \frac{a^x}{\ln a} + C$
5. $\int \sin x \, dx = -\cos x + C$
6. $\int \cos x \, dx = \sin x + C$
7. $\int \sec^2 x \, dx = \tan x + C$
8. $\int \csc^2 x \, dx = -\cot x + C$
9. $\int \sec x \tan x \, dx = \sec x + C$
10. $\int \csc x \cot x \, dx = -\csc x + C$
11. $\int \cot x \, dx = \ln |\sin x| + C$
12. $\int \tan x \, dx = -\ln |\cos x| + C = \ln |\sec x| + C$
13. $\int \sec x \, dx = \ln |\sec x + \tan x| + C$
14. $\int \csc x \, dx = \ln |\csc x - \cot x| + C$

---

Inverse Trigonometric Integrals

1. $\int \frac{1}{\sqrt{a^2 - x^2}} \, dx = \sin^{-1} \left(\frac{x}{a}\right) + C$
2. $\int \frac{-1}{\sqrt{a^2 - x^2}} \, dx = \cos^{-1} \left(\frac{x}{a}\right) + C$
3. $\int \frac{1}{x^2 + a^2} \, dx = \frac{1}{a} \tan^{-1} \left(\frac{x}{a}\right) + C$
4. $\int \frac{-1}{x^2 + a^2} \, dx = \frac{1}{a} \cot^{-1} \left(\frac{x}{a}\right) + C$
5. $\int \frac{1}{x \sqrt{x^2 + a^2}} \, dx = \frac{1}{a} \sec^{-1} \left|\frac{x}{a}\right| + C$
6. $\int \frac{-1}{x \sqrt{x^2 - a^2}} \, dx = \frac{-1}{a} \csc^{-1} \left|\frac{x}{a}\right| + C$

---

Logarithmic and Advanced Integrals

1. $\int e^{x} f(x) + f'(x) \, dx = e^x f(x) + C$
2. $\int \frac{dx}{x^2 + a^2} = \frac{1}{a} \ln |x + \sqrt{x^2 + a^2}| + C$
3. $\int \frac{dx}{x^2 - a^2} = \frac{1}{2a} \ln \left|\frac{x - a}{x + a}\right| + C$
4. $\int \frac{dx}{a^2 - x^2} = \frac{1}{2a} \ln \left|\frac{a + x}{a - x}\right| + C$
5. $\int \frac{dx}{a^2 - x^2} = \frac{1}{2a} \ln \left|\frac{a + x}{x - a}\right| + C$

---

Additional Properties

• $\int k f(x) \, dx = k \int f(x) \, dx$
• $\int [f(x) \pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx$
• $\int c \, dx = c x + C$

Line Equations

1. $ax + by + c=0$

   $m = -a/b$ (Slope of line)

2. One Point form of line

$$

y - y_1 = m (x-x_1)
$$

1. Two point form of line

$$ y-y_1 = \frac{y_2-y_1}{x_2-x_1}{x-x_1} $$

1. Intercept Form of line

$$ \frac{x}{a} + \frac{y}{b} = 1 $$

1. Normal form of line

$$ x\cos \theta + y\sin\theta = P $$

1. Point Slope form

$$ y = mx+ c \\ \text{Where $m$ is slope of line defined as } m = \frac{y_2 - y_1}{x_2 - x_1} $$

Distance of a point from a line

$$ \text{Dist}_{PA}= \Bigg|{\frac{ax_1 + by_1 + c}{\sqrt{a^2+b^2}}}\Bigg| $$

Distance between two lines

$y = mx + c_1 \qquad y= mx+c_2$

$$ \text{d} = \Bigg| \frac{c_1 - c_2}{\sqrt{1+m^2}}\Bigg| = \Bigg|\frac{c_1 - c_2}{\sqrt{a^2+b^2}}\Bigg| $$

Angle between two lines

Where $m_1$ and $m_2$ are slopes of two lines.

$$ \tan\theta = \frac{m_2 - m_1}{1+m_2m_1} $$

• If line $l_1$ and $l_2$ are orthogonal to each other, then. $m_1m_2 = -1$
• Collinearity of points

Slope of $AB$ = Slope of $AC$

Shapes CSA(Curved Surface Area), T(Total)SA, and volume

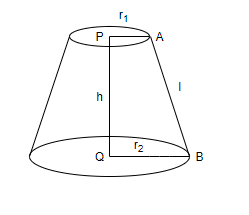
Frustum

$\text{CSA} = \pi l (r_1+ r_2)$

$\text{TSA} = \pi r_1^2 + \pi r_2^2 + \pi l(r_1+r_2)$

$\text{Volume} = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1r_2)$

where $l= \sqrt{h^2+(r_1-r_2)^2}$

Adjoint and Inverse

$A(\text{adj} A) = \|A\| I_n = (\text{adj}) A$

$A^{-1} = \frac{1}{\|A\|} (\text{adj} A)$

$(A^\top)^{-1} = (A^{-1})^\top$

$\|A \enspace adj A\| = \|A\|^{n}$

$\|A^\top\| = \|A\| $

$AA^{-1} = I_n$

$(A^{-1})^{-1} = A$

$(AB)^{-1} = B^{-1}A^{-1}$

$\text{adj}\space AB = (\text{adj} B)(\text{adj} A)$

$\|AB\| = \|A\| \|B\|$

$\text{adj}A^\top = (\text{adj} A)\top$

$\|KA\| = K^n \|A\|$

$AA^{-1}=I$

$A^{-1}I = A^{-1}$

$\|\text{adj} A\| = \|A\|^{n-1}$

$\text{adj} \space(adj A) = \|A\|^{n-2} A$

$\|\text{adj} \space(adj A)\| = \|A\|^{(n-1)^{2}}$

Binomial Theorem

Initial conditions:

$^nc_0 = 1$

$^nc_1 = n$

$^nc_n = 1$

$^nc_{n-1} = n$

Basic expansion:

$$(x+a)^n = {^nc_0}x^na^0 + {^nc_1}x^{n-1}a^1 + {^nc_2}x^{n-2}a^2 + ... + {^nc_n}x^0a^n$$

Sum and difference formulas:

$$(x+a)^n + (x-a)^n = 2[{^nc_0}x^na^0 + {^nc_2}x^{n-2}a^2 + {^nc_4}x^{n-4}a^4 + ...]$$ $$(x+a)^n - (x-a)^n = 2[{^nc_1}x^{n-1}a^1 + {^nc_3}x^{n-3}a^3 + {^nc_5}x^{n-5}a^5 + ...]$$

Number of terms:

	When n is odd	When n is even
(x+a)^n + (x-a)^n	$(\frac{n+1}{2})$ terms	$(\frac{n}{2})$ terms
(x+a)^n - (x-a)^n	$(\frac{n+1}{2})$ terms	$(\frac{n}{2})$ terms

General Term and Middle Term

General term: $t_{r+1} = {^nc_r}x^{n-r}a^r$

Middle term occurs at:

• If n is odd: $(\frac{n+1}{2})$ & $(\frac{n+3}{2})$ terms

• If n is even: $(\frac{n}{2}+1)$ terms

Coefficient Tables

Coefficient of	Binomial Expression	is
$(r+1)^{\text{th}}$	$(1+x)^n$	${^nc_r}$
$x^r$	$(1+x)^n$	${^nc_r}$
$x^r$	$(1-x)^n$	$(-1)^r\enspace{^nc_r}$
$(r+1)^{\text{th}}$	$(1-x)^n$	$(-1)^r\enspace{^nc_r}$

Relations

$\frac{^nc_r}{^nc_{r-1}} = \frac{n-r+1}{r}$

$^nc_r = (\frac{n}{r})\enspace{^{n-1}c_{r-1}}$

$\frac{^nc_{r+1}}{^nc_r} = \frac{n-r}{r+1}$

$\frac{t_{r+1}}{t_r} = \frac{n-r+1}{r} \cdot \frac{a}{x}$

Probability

$P_r = \frac{n!}{(n-r)!}$

$C_r = \frac{n!}{(n-r)!r!}$

Operation	Notation
A or B	$A \cup B$
A and B	$A \cap B$
A but not B	$A \cap \bar{B}$
B but not A	$\bar{A} \cap B$
Neither A nor B	$\bar{A} \cap \bar{B}$
At least one of A,B,& C	$A \cup B \cup C$
Exactly one of A,B	$(A \cap \bar{B}) \cup (\bar{A} \cap B)$
All Three of A,B,& C	$A \cap B \cap C$
Exactly Two of A,B,& C	$(A \cap B \cap \bar{C}) \cup (A \cap \bar{B} \cap C) \cup (\bar{A} \cap B \cap C)$
Exactly One of A,B,& C	$(A \cap \bar{B} \cap \bar{C}) \cup (\bar{A} \cap B \cap \bar{C}) \cup (\bar{A} \cap \bar{B} \cap C)$

The probability formulas:

$$ \begin{split} P(A \cup B) &= P(A) + P(B) - P(A \cap B) \\ &= 1 - P(\overline{A \cup B}) \\ &= 1 - P(\overline{A} \cap \overline{B}) \\ &= 1 - P(\bar{A})P(\bar{B}) \end{split} $$

$$ \tag{A and B\\ are mutually exclusive} P(A \cup B) = P(A) + P(B) $$

$$ \begin{split} P(A \cup B \cup C) &= P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C) - P(A \cap C) + P(A \cap B \cap C) \end{split} $$

$$ \tag{A,B and C\\ are mutually exclusive} P(A \cup B \cup C) = P(A) + P(B) + P(C) $$

• Probability of occurrence of (A) only $$P(A \cap \bar{B}) = P(A) - P(A \cap B)$$

• Probability of occurrence of (B) only $$P(\bar{A} \cap B) = P(B) - P(A \cap B)$$

• P of occurrence of exactly one of A and B $$P(A \cap \bar{B}) \cup P(\bar{A} \cap B) \Rightarrow P(A \cup B) - P(A \cap B)$$

• Three Events Occurring Simultaneously

$$P(A \cup B \cup C)$$

• At Least Two Events: $$P(A \cap B) + P(B \cap C) + P(C \cap A) - 2P(A \cap B \cap C)$$

• Exactly Two Out of Three Events: $$P(A \cap B) + P(B \cap C) + P(C \cap A) - 3P(A \cap B \cap C)$$

• Exactly One Out of Three Events: $$P(A) + P(B) + P(C) - 2P(A \cap B) - 2P(B \cap C) - 2P(C \cap A) + 3P(A \cap B \cap C)$$

• Exactly One Out of Two Events $$P(A \cap \overline{B}) + P(\overline{A} \cap B)$$

  • Simplified Form: $$P(A) + P(B) - 2P(A \cap B) \implies P(A \cup B) - P(A \cap B)$$

• Conditional probability P of E given A is true

$$ \begin{split} P(E_i|A) &= P(E_i)P(A|E_i) \\ &= \sum_{i=1}^n P(E_i)P(A|E_i) \end{split} $$

$P(A \cap B) = P(A)P(B|A) = P(B)P(A|B)$

$P(A \cap B \cap C \cap D) = P(A)P(B|A)P(C|A \cap B)P(D|A \cap B \cap C)$

$$P(E_i | A) = \frac{P(E_i) P(A|E_i)}{\sum^n_{i=1}P(E_i) P(A|E_i)}$$

Also noting the card suit groupings shown in the image:

• Hearts and Diamonds are grouped as Red
• Spades and Clubs are grouped as Black

Mean Variance & Standard Deviation

• $p$ means success event
• $q$ means not a sucess event

$P(X = r) = {}_nC_r p^r q^{n-r}$

$Variance = npq$

$Mean = np$

Probability Relations: $$P(X \leq x_i) = P(X = x_1) + P(X = x_2) + ... + P(X = x_i) = p_1 + p_2 + ... + p_i$$

$$P(X < x_i) = P(X = x_1) + P(X = x_2) + ... + P(X = x_{i-1}) = p_1 + p_2 + ... + p_{i-1}$$

$$P(X \geq x_i) = P(X = x_i) + P(X = x_{i+1}) + ... + P(X = x_n) = p_i + p_{i+1} + ... + p_n$$

$$P(X > x_i) = P(X = x_{i+1}) + P(X = x_{i+2}) + ... + P(X = x_n) = p_{i+1} + p_{i+2} + ... + p_n$$

$P(X \geq x_i) = 1 - P(X < x_i)$

$P(X \leq x_i) = 1 - P(X > x_i)$

$P(X > x_i) = 1 - P(X \leq x_i)$

$P(X < x_i) = 1 - P(X \geq x_i)$

$$P(x_i \leq X \leq x_j) = P(X = x_i) + P(X = x_{i+1}) + ... + P(X = x_j)$$

$$P(x_i < X < x_j) = P(X = x_{i+1}) + P(X = x_{i+2}) + ... + P(X = x_{j-1})$$

Mean Formulas(Matehmatical expectation):

• where $f$ = frequency

$$ \begin{split} \overline{X} &= p_1x_1 + p_2x_2 + ... + p_nx_n \\ &= E(X) \\ &= \sum_{i=1}^n p_ix_i \\ &= \frac{f_1x_1}{N} + \frac{f_2x_2}{N} + ... + \frac{f_nx_n}{N} \end{split} $$

$$p_i = \frac{f_i}{N}$$

Variance Formula:

$$ \begin{split} Var(X) &= E(X^2) - \lbrace E(X)\rbrace^2 \\ &= \sum_{i=1}^n p_ix_i^2 - (\sum_{i=1}^n p_ix_i)^2 \end{split} $$

$$\frac{\sum x^2}{n} - (\frac{\sum x}{n})^2$$

Random Variable Property:

If $aX + b$ is a random variable with mean $aX + B$ and variance $a^2Var(X)$

Standard Deviation:

$$ \sigma = \sqrt{Var(X)} \newline\qquad \sigma^2 = \frac{1}{N^2} \lbrack N\sum*{i=1}^n fx_i^2 - (\sum*{i=1}^n fx_i)^2 \rbrack $$

---

Arithmetic Progression (AP)

• General Form: $A, B, C$

$$2B = A + C$$

Formulas:

• $t_n = a + (n-1)d$
• $S_n = \frac{n}{2} \left[2a + (n-1)d \right]$
• $S_n = \frac{n}{2} [a + a_n]$
• $t_n = S_n - S_{n-1}$

Arithmetic Mean (AM):

$G = \frac{a+b}{2}$

---

Geometric Progression (GP)

• General Form: $A, B, C$

$$B^2 = A \cdot C$$

Formulas:

• $t_n = a \cdot r^{n-1}$
• $S_n = a \frac{r^n - 1}{r - 1}, \, r \neq 1$

• $S_\infty = \frac{a}{r-1}, \, |r| < 1$

• where $r$ is common ratio

Geometric Mean (GM):

• Single Mean Between $a$ and $b$: $G = \sqrt{ab}$
• Multiple Means:
• $G_1 = ar^1$
• $G_2 = ar^2$
• $G_3 = ar^3$
• $r = \sqrt[n+1]{\frac{b}{a}}$

---

AP, GP, HP Relation:

$$AP \geq GP \geq HP$$

---

Special Sequences:

1. Sum of Natural Numbers:

$$ 1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2} $$

1. Sum of Squares of Natural Numbers:

$$ 1^2 + 2^2 + 3^2 + \dots + n^2 = \frac{n(n+1)(2n+1)}{6} $$

1. Sum of Cubes of Natural Numbers:

$$ 1^3 + 2^3 + 3^3 + \dots + n^3 = \left[\frac{n(n+1)}{2}\right]^2 $$

Homogeneous and Non homogeneous equations solutions

NON-HOMOGENEOUS

$AX = B$

Unique Solution

1. $\text{adj}(A)B = 0 \implies \text{Infinite Solutions}$
2. $\text{adj}(A)B \neq 0 \implies \text{No Solution}$

 

 

When $|A| \neq 0$

 

When $|A| = 0$

HOMOGENEOUS

$AX = 0$

Trivial solution $x = y = z = 0 \enspace $:

1. $\text{Infinite Solutions}$ put $z = k$ and solve

---

Finding Log

1. Given we need to find $\log$ of $\log 15.27$

   • Move the decimal after 1st digit and introduce power of 10.

   $$ \log \textcolor{#f56c42}1.\textcolor{#f56c42}5\textcolor{#ad42f5}2\textcolor{#f542bc}7 \times 10^{\textcolor{#42f5f2}1} $$

   When the decimal is moved in left/right: $$ (-)\medspace \overrightarrow{\text{introduce negative powers}} \qquad \overleftarrow{\text{introduce positive powers}} \medspace(+) $$

2. Look for $\textcolor{#f56c42}{15}$^th row and column with label $\textcolor{#ad42f5}2$. which is $\bold{\textcolor{#07fc03}{1818}}$.

3. Add Mean difference from column $\textcolor{#f542bc}7$ in the corresponding row. which is $\textcolor{#07fc03}{20}$

   $$ 1818 + 20 = \bold{\textcolor{#07fc03}{1838}} $$

4. Write the exponent, insert decimal and write the value calculated in Step 3.

   $$ \textcolor{#42f5f2}1.\textcolor{#07fc03}{1838} $$

5. So $\log 15.27 = \bold{\textcolor{#07fc03}{1.1838}}$

Finding AntiLog

1. Given we need to find Antilog of $15.5932$ $$ \log k = 15.5932 \\ k = Antilog (\medspace \textcolor{#42f5f2}{15}\textcolor{#f56c42}{.59}\textcolor{#ad42f5}3\textcolor{#f542bc}2\medspace) $$

2. Look for $0\textcolor{#f56c42}{.59}$^th row and column with label $\textcolor{#ad42f5}3$. Which is $\bold{\textcolor{#07fc03}{3917}}$.

3. Add Mean difference from column $\textcolor{#f542bc}2$ to previous result. Which is $\textcolor{#07fc03}2$

   $$ 3917 + 2 = \bold{\textcolor{#07fc03}{3919}} $$

4. Add $1$ to characteristic $\textcolor{#42f5f2}{15} = \textcolor{#07fc03}{16}$ and add insert the decimal from left calculated in step 2. That means we need to add decimal after $\textcolor{#07fc03}{16}$^th position

   $$ 3919\enspace0000\enspace0000\enspace000 .\\ \implies k = \bold{\textcolor{#07fc03}{3.919\times10^{15}}} $$

Quickly write the exponential form

Since, we want to put decimal just after 1^st digit. We need to move decimal from 16^th position to right after 1^st digit; which will introduce +ve powers. ($16 -1 = \textcolor{#07fc03}{15}$). Since we moved 15 positions left.

$3.919 \times 10^{\textcolor{#07fc03}{15}}$